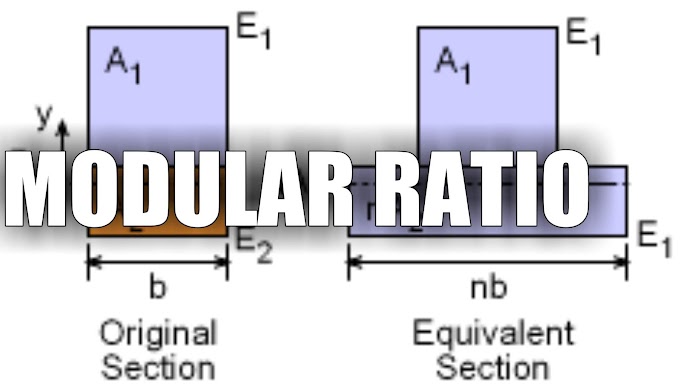
The modular ratio is the ratio of the modulus of elasticity of two different materials. If E1 and E2 are Young's modulus of two materials, then the ratio E1/E2 or E2/E1 is known as modular ratio.
 |
In structures involving composite materials, this modular ratio plays a significant role in the load shared by the materials. In the elastic theory, structures having different materials are made equivalent to one common material to calculate the amount of load shared by the individual materials. An example of this is reinforced concrete structures.
Modular Ratio in RCC is defined as the ratio between Modulus of Elasticity of Steel and Modulus of Elasticity of Concrete (Es/Ec). Where Es is the modulus of elasticity of steel which is 2,00,000 N/mm2. However concrete does not have a definite value of modulus of elasticity as it is not a perfectly elastic material. Though the short-term modulus of concrete can be approximately calculated (i.e. Ec = 5000√fck N/mm2, where fck is the characteristic strength of concrete) it does not take into account the effects of creep, shrinkage and other long-term effects. So, it can not be considered in calculating the modular ratio.
In the working stress method, the modular ratio is assumed to have a value of 280/3σcbc, where σcbc is the permissible compressive stress (in N/mm2) in concrete due in bending.



0 Comments